9 210: Functional enrichment analysis of high-throughput omics data
9.1 Instructor names and contact information
- Ludwig Geistlinger (Ludwig.Geistlinger@sph.cuny.edu)
- Levi Waldron
CUNY School of Public Health 55 W 125th St, New York, NY 10027
9.2 Workshop Description
This workshop gives an in-depth overview of existing methods for enrichment analysis of gene expression data with regard to functional gene sets, pathways, and networks. The workshop will help participants understand the distinctions between assumptions and hypotheses of existing methods as well as the differences in objectives and interpretation of results. It will provide code and hands-on practice of all necessary steps for differential expression analysis, gene set- and network-based enrichment analysis, and identification of enriched genomic regions and regulatory elements, along with visualization and exploration of results.
9.2.1 Pre-requisites
- Basic knowledge of R syntax
- Familiarity with the SummarizedExperiment class
Familiarity with the GenomicRanges class
- Familiarity with high-throughput gene expression data as obtained with microarrays and RNA-seq
Familiarity with the concept of differential expression analysis (with e.g. limma, edgeR, DESeq2)
9.2.2 Workshop Participation
Execution of example code and hands-on practice
9.2.3 R / Bioconductor packages used
9.2.4 Time outline
| Activity | Time |
|---|---|
| Background | 30m |
| Differential expression analysis | 15m |
| Gene set analysis | 30m |
| Gene network analysis | 15m |
| Genomic region analysis | 15m |
9.3 Goals and objectives
Theory:
- Gene sets, pathways & regulatory networks
- Resources
- Gene set analysis vs. gene set enrichment analysis
- Underlying null: competitive vs. self-contained
- Generations: ora, fcs & topology-based
Practice:
- Data types: microarray vs. RNA-seq
- Differential expression analysis
- Defining gene sets according to GO and KEGG
- GO/KEGG overrepresentation analysis
- Functional class scoring & permutation testing
- Network-based enrichment analysis
- Genomic region enrichment analysis
9.4 Where does it all come from?
Test whether known biological functions or processes are over-represented (= enriched) in an experimentally-derived gene list, e.g. a list of differentially expressed (DE) genes. See Goeman and Buehlmann, 2007 for a critical review.
Example: Transcriptomic study, in which 12,671 genes have been tested for differential expression between two sample conditions and 529 genes were found DE.
Among the DE genes, 28 are annotated to a specific functional gene set, which contains in total 170 genes. This setup corresponds to a 2x2 contingency table,
deTable <-
matrix(c(28, 142, 501, 12000),
nrow = 2,
dimnames = list(c("DE", "Not.DE"),
c("In.gene.set", "Not.in.gene.set")))
deTable
#> In.gene.set Not.in.gene.set
#> DE 28 501
#> Not.DE 142 12000where the overlap of 28 genes can be assessed based on the hypergeometric distribution. This corresponds to a one-sided version of Fisher’s exact test, yielding here a significant enrichment.
fisher.test(deTable, alternative = "greater")
#>
#> Fisher's Exact Test for Count Data
#>
#> data: deTable
#> p-value = 4.088e-10
#> alternative hypothesis: true odds ratio is greater than 1
#> 95 percent confidence interval:
#> 3.226736 Inf
#> sample estimates:
#> odds ratio
#> 4.721744This basic principle is at the foundation of major public and commercial enrichment tools such as DAVID and Pathway Studio.
Although gene set enrichment methods have been primarily developed and applied on transcriptomic data, they have recently been modified, extended and applied also in other fields of genomic and biomedical research. This includes novel approaches for functional enrichment analysis of proteomic and metabolomic data as well as genomic regions and disease phenotypes, Lavallee and Yates, 2016, Chagoyen et al., 2016, McLean et al., 2010, Ried et al., 2012.
9.5 Gene expression-based enrichment analysis
The first part of the workshop is largely based on the EnrichmentBrowser package, which implements an analysis pipeline for high-throughput gene expression data as measured with microarrays and RNA-seq. In a workflow-like manner, the package brings together a selection of established Bioconductor packages for gene expression data analysis. It integrates a wide range of gene set enrichment analysis methods and facilitates combination and exploration of results across methods.

suppressPackageStartupMessages(library(EnrichmentBrowser))Further information can be found in the vignette and publication.
9.6 A primer on terminology, existing methods & statistical theory
Gene sets, pathways & regulatory networks
Gene sets are simple lists of usually functionally related genes without further specification of relationships between genes.
Pathways can be interpreted as specific gene sets, typically representing a group of genes that work together in a biological process. Pathways are commonly divided in metabolic and signaling pathways. Metabolic pathways such as glycolysis represent biochemical substrate conversions by specific enzymes. Signaling pathways such as the MAPK signaling pathway describe signal transduction cascades from receptor proteins to transcription factors, resulting in activation or inhibition of specific target genes.
Gene regulatory networks describe the interplay and effects of regulatory factors (such as transcription factors and microRNAs) on the expression of their target genes.
Resources
GO and KEGG annotations are most frequently used for the enrichment analysis of functional gene sets. Despite an increasing number of gene set and pathway databases, they are typically the first choice due to their long-standing curation and availability for a wide range of species.
GO: The Gene Ontology (GO) consists of three major sub-ontologies that classify gene products according to molecular function (MF), biological process (BP) and cellular component (CC). Each ontology consists of GO terms that define MFs, BPs or CCs to which specific genes are annotated. The terms are organized in a directed acyclic graph, where edges between the terms represent relationships of different types. They relate the terms according to a parent-child scheme, i.e. parent terms denote more general entities, whereas child terms represent more specific entities.
KEGG: The Kyoto Encyclopedia of Genes and Genomes (KEGG) is a collection of manually drawn pathway maps representing molecular interaction and reaction networks. These pathways cover a wide range of biochemical processes that can be divided in 7 broad categories: metabolism, genetic and environmental information processing, cellular processes, organismal systems, human diseases, and drug development. Metabolism and drug development pathways differ from pathways of the other 5 categories by illustrating reactions between chemical compounds. Pathways of the other 5 categories illustrate molecular interactions between genes and gene products.
Gene set analysis vs. gene set enrichment analysis
The two predominantly used enrichment methods are:
- Overrepresentation analysis (ORA), testing whether a gene set contains disproportional many genes of significant expression change, based on the procedure outlined in the first section
- Gene set enrichment analysis (GSEA), testing whether genes of a gene set accumulate at the top or bottom of the full gene vector ordered by direction and magnitude of expression change Subramanian et al., 2005
However, the term gene set enrichment analysis nowadays subsumes a general strategy implemented by a wide range of methods Huang et al., 2009. Those methods have in common the same goal, although approach and statistical model can vary substantially Goeman and Buehlmann, 2007, Khatri et al., 2012.
To better distinguish from the specific method, some authors use the term gene set analysis to denote the general strategy. However, there is also a specific method from Efron and Tibshirani, 2007 of this name.
Underlying null: competitive vs. self-contained
Goeman and Buehlmann, 2007 classified existing enrichment methods into competitive and self-contained based on the underlying null hypothesis.
- Competitive null hypothesis: the genes in the set of interest are at most as often DE as the genes not in the set,
- Self-contained null hypothesis: no genes in the set of interest are DE.
Although the authors argue that a self-contained null is closer to the actual question of interest, the vast majority of enrichment methods is competitive.
Goeman and Buehlmann further raise several critical issues concerning the 2x2 ORA:
- rather arbitrary classification of genes in DE / not DE
- based on gene sampling, although sampling of subjects is appropriate
- unrealistic independence assumption between genes, resulting in highly anti-conservative p-values
With regard to these statistical concerns, GSEA is considered superior:
- takes all measured genes into account
- subject sampling via permutation of class labels
- the incorporated permutation procedure implicitly accounts for correlations between genes
However, the simplicity and general applicability of ORA is unmet by subsequent methods improving on these issues. For instance, GSEA requires the expression data as input, which is not available for gene lists derived from other experiment types. On the other hand, the involved sample permutation procedure has been proven inaccurate and time-consuming Efron and Tibshirani, 2007, Phipson and Smyth, 2010, Larson and Owen, 2015.
Generations: ora, fcs & topology-based
Khatri et al., 2012 have taken a slightly different approach by classifying methods along the timeline of development into three generations:
- Generation: ORA methods based on the 2x2 contingency table test,
- Generation: functional class scoring (FCS) methods such as GSEA, which compute gene set (= functional class) scores by summarizing per-gene DE statistics,
- Generation: topology-based methods, explicitly taking into account interactions between genes as defined in signaling pathways and gene regulatory networks (Geistlinger et al., 2011 for an example).
Although topology-based (also: network-based) methods appear to be most realistic, their straightforward application can be impaired by features that are not-detectable on the transcriptional level (such as protein-protein interactions) and insufficient network knowledge Geistlinger et al., 2013, Bayerlova et al., 2015.
Given the individual benefits and limitations of existing methods, cautious interpretation of results is required to derive valid conclusions. Whereas no single method is best suited for all application scenarios, applying multiple methods can be beneficial. This has been shown to filter out spurious hits of individual methods, thereby reducing the outcome to gene sets accumulating evidence from different methods Geistlinger et al., 2016, Alhamdoosh et al., 2017.
9.7 Data types
Although RNA-seq (read count data) has become the de facto standard for transcriptomic profiling, it is important to know that many methods for differential expression and gene set enrichment analysis have been originally developed for microarray data (intensity measurements).
However, differences in data distribution assumptions (microarray: quasi-normal, RNA-seq: negative binomial) made adaptations in differential expression analysis and, to some extent, also in gene set enrichment analysis necessary.
Thus, we consider two example datasets - a microarray and a RNA-seq dataset, and discuss similarities and differences of the respective analysis steps.
For microarray data, we consider expression measurements of patients with acute lymphoblastic leukemia Chiaretti et al., 2004. A frequent chromosomal defect found among these patients is a translocation, in which parts of chromosome 9 and 22 swap places. This results in the oncogenic fusion gene BCR/ABL created by positioning the ABL1 gene on chromosome 9 to a part of the BCR gene on chromosome 22.
We load the ALL dataset
library(ALL)
data(ALL)and select B-cell ALL patients with and without the BCR/ABL fusion, as described previously Gentleman et al., 2005.
ind.bs <- grep("^B", ALL$BT)
ind.mut <- which(ALL$mol.biol %in% c("BCR/ABL", "NEG"))
sset <- intersect(ind.bs, ind.mut)
all.eset <- ALL[, sset]We can now access the expression values, which are intensity measurements on a log-scale for 12,625 probes (rows) across 79 patients (columns).
dim(all.eset)
#> Features Samples
#> 12625 79
exprs(all.eset)[1:4,1:4]
#> 01005 01010 03002 04007
#> 1000_at 7.597323 7.479445 7.567593 7.905312
#> 1001_at 5.046194 4.932537 4.799294 4.844565
#> 1002_f_at 3.900466 4.208155 3.886169 3.416923
#> 1003_s_at 5.903856 6.169024 5.860459 5.687997As we often have more than one probe per gene, we compute gene expression values as the average of the corresponding probe values.
allSE <- probe2gene(all.eset)
head(names(allSE))
#> [1] "5595" "7075" "1557" "643" "1843" "4319"For RNA-seq data, we consider transcriptome profiles of four primary human airway smooth muscle cell lines in two conditions: control and treatment with dexamethasone Himes et al., 2014.
We load the airway dataset
library(airway)
data(airway)For further analysis, we only keep genes that are annotated to an ENSEMBL gene ID.
airSE <- airway[grep("^ENSG", names(airway)), ]
dim(airSE)
#> [1] 63677 8assay(airSE)[1:4,1:4]
#> SRR1039508 SRR1039509 SRR1039512 SRR1039513
#> ENSG00000000003 679 448 873 408
#> ENSG00000000005 0 0 0 0
#> ENSG00000000419 467 515 621 365
#> ENSG00000000457 260 211 263 1649.8 Differential expression analysis
Normalization of high-throughput expression data is essential to make results within and between experiments comparable. Microarray (intensity measurements) and RNA-seq (read counts) data typically show distinct features that need to be normalized for. As this is beyond the scope of this workshop, we refer to limma for microarray normalization and EDASeq for RNA-seq normalization. See also EnrichmentBrowser::normalize, which wraps commonly used functionality for normalization.
The EnrichmentBrowser incorporates established functionality from the limma package for differential expression analysis. This involves the voom transformation when applied to RNA-seq data. Alternatively, differential expression analysis for RNA-seq data can also be carried out based on the negative binomial distribution with edgeR and DESeq2.
This can be performed using the function EnrichmentBrowser::deAna and assumes some standardized variable names:
- GROUP defines the sample groups being contrasted,
- BLOCK defines paired samples or sample blocks, as e.g. for batch effects.
For more information on experimental design, see the limma user’s guide, chapter 9.
For the ALL dataset, the GROUP variable indicates whether the BCR-ABL gene fusion is present (1) or not (0).
allSE$GROUP <- ifelse(allSE$mol.biol == "BCR/ABL", 1, 0)
table(allSE$GROUP)
#>
#> 0 1
#> 42 37For the airway dataset, it indicates whether the cell lines have been treated with dexamethasone (1) or not (0).
airSE$GROUP <- ifelse(colData(airway)$dex == "trt", 1, 0)
table(airSE$GROUP)
#>
#> 0 1
#> 4 4Paired samples, or in general sample batches/blocks, can be defined via a BLOCK column in the colData slot. For the airway dataset, the sample blocks correspond to the four different cell lines.
airSE$BLOCK <- airway$cell
table(airSE$BLOCK)
#>
#> N052611 N061011 N080611 N61311
#> 2 2 2 2For microarray data, the EnrichmentBrowser::deAna function carries out differential expression analysis based on functionality from the limma package. Resulting log2 fold changes and t-test derived p-values for each gene are appended to the rowData slot.
allSE <- deAna(allSE)
rowData(allSE, use.names=TRUE)
#> DataFrame with 9010 rows and 3 columns
#> FC ADJ.PVAL limma.STAT
#> <numeric> <numeric> <numeric>
#> 5595 0.0429698599842595 0.899246817310775 0.734679177472013
#> 7075 0.0320835027449625 0.949001013642671 0.4546910829318
#> 1557 -0.0439401425131442 0.818330132411339 -1.06578261967549
#> 643 -0.0277543539240438 0.929148567589577 -0.567394394416651
#> 1843 -0.427302534257363 0.566034751753148 -1.75050227190017
#> ... ... ... ...
#> 6300 -0.026651766164237 0.922828548631225 -0.608608859328046
#> 7297 -0.124257678078831 0.804578494190681 -1.11279493778184
#> 2246 0.0522428857778935 0.748021044717352 1.27408420746691
#> 7850 -0.00908229596065303 0.991826450687159 -0.102406339091096
#> 1593 -0.00747713820802068 0.989532971314233 -0.145650256847251Nominal p-values are already corrected for multiple testing (ADJ.PVAL) using the method from Benjamini and Hochberg implemented in stats::p.adjust.
For RNA-seq data, the deAna function can be used to carry out differential expression analysis between the two groups either based on functionality from limma (that includes the voom transformation), or alternatively, the frequently used edgeR or DESeq2 package. Here, we use the analysis based on edgeR.
airSE <- deAna(airSE, de.method="edgeR")
#> Excluding 50740 genes not satisfying min.cpm thresholdrowData(airSE, use.names=TRUE)
#> DataFrame with 12937 rows and 3 columns
#> FC ADJ.PVAL
#> <numeric> <numeric>
#> ENSG00000000003 -0.404945626610932 0.00213458295385943
#> ENSG00000000419 0.182985434777532 0.0915691945172958
#> ENSG00000000457 0.0143477674070903 0.922279475399443
#> ENSG00000000460 -0.141173372957311 0.619013213521635
#> ENSG00000000971 0.402240426474172 0.00403820532305827
#> ... ... ...
#> ENSG00000273270 -0.129793853337261 0.495892935815041
#> ENSG00000273290 0.505580471641003 0.00639218387702899
#> ENSG00000273311 0.00161557580855148 0.996356136956657
#> ENSG00000273329 -0.222817127090519 0.388294594068803
#> ENSG00000273344 0.0151704005097403 0.962777106053257
#> edgeR.STAT
#> <numeric>
#> ENSG00000000003 35.8743710016552
#> ENSG00000000419 5.90960619951737
#> ENSG00000000457 0.0233923316990905
#> ENSG00000000460 0.492929955080604
#> ENSG00000000971 27.8509962017407
#> ... ...
#> ENSG00000273270 0.901598359265205
#> ENSG00000273290 23.0905678847871
#> ENSG00000273311 8.04821152029429e-05
#> ENSG00000273329 1.42723325850597
#> ENSG00000273344 0.00543503273765429Exercise: Compare the number of differentially expressed genes as obtained on the airSE with limma/voom, edgeR, and DESeq2.
9.9 Gene sets
We are now interested in whether pre-defined sets of genes that are known to work together, e.g. as defined in the Gene Ontology or the KEGG pathway annotation, are coordinately differentially expressed.
The function getGenesets can be used to download gene sets from databases such as GO and KEGG. Here, we use the function to download all KEGG pathways for a chosen organism (here: ) as gene sets.
kegg.gs <- getGenesets(org="hsa", db="kegg")Analogously, the function getGenesets can be used to retrieve GO terms of a selected ontology (here: biological process, BP) as defined in the GO.db annotation package.
go.gs <- getGenesets(org="hsa", db="go", go.onto="BP", go.mode="GO.db")
#> If provided a file, the function getGenesets parses user-defined gene sets from GMT file format. Here, we use this functionality for reading a list of already downloaded KEGG gene sets for Homo sapiens containing NCBI Entrez Gene IDs.
data.dir <- system.file("extdata", package="EnrichmentBrowser")
gmt.file <- file.path(data.dir, "hsa_kegg_gs.gmt")
hsa.gs <- getGenesets(gmt.file)
hsa.gs[1:2]
#> $hsa05416_Viral_myocarditis
#> [1] "100509457" "101060835" "1525" "1604" "1605"
#> [6] "1756" "1981" "1982" "25" "2534"
#> [11] "27" "3105" "3106" "3107" "3108"
#> [16] "3109" "3111" "3112" "3113" "3115"
#> [21] "3117" "3118" "3119" "3122" "3123"
#> [26] "3125" "3126" "3127" "3133" "3134"
#> [31] "3135" "3383" "3683" "3689" "3908"
#> [36] "4624" "4625" "54205" "5551" "5879"
#> [41] "5880" "5881" "595" "60" "637"
#> [46] "6442" "6443" "6444" "6445" "71"
#> [51] "836" "841" "842" "857" "8672"
#> [56] "940" "941" "942" "958" "959"
#>
#> $`hsa04622_RIG-I-like_receptor_signaling_pathway`
#> [1] "10010" "1147" "1432" "1540" "1654" "23586" "26007"
#> [8] "29110" "338376" "340061" "3439" "3440" "3441" "3442"
#> [15] "3443" "3444" "3445" "3446" "3447" "3448" "3449"
#> [22] "3451" "3452" "3456" "3467" "3551" "3576" "3592"
#> [29] "3593" "3627" "3661" "3665" "4214" "4790" "4792"
#> [36] "4793" "5300" "54941" "55593" "5599" "5600" "5601"
#> [43] "5602" "5603" "56832" "57506" "5970" "6300" "64135"
#> [50] "64343" "6885" "7124" "7186" "7187" "7189" "7706"
#> [57] "79132" "79671" "80143" "841" "843" "8517" "8717"
#> [64] "8737" "8772" "9140" "9474" "9636" "9641" "9755"hsa.gs[1:2]
#> $hsa05416_Viral_myocarditis
#> [1] "100509457" "101060835" "1525" "1604" "1605"
#> [6] "1756" "1981" "1982" "25" "2534"
#> [11] "27" "3105" "3106" "3107" "3108"
#> [16] "3109" "3111" "3112" "3113" "3115"
#> [21] "3117" "3118" "3119" "3122" "3123"
#> [26] "3125" "3126" "3127" "3133" "3134"
#> [31] "3135" "3383" "3683" "3689" "3908"
#> [36] "4624" "4625" "54205" "5551" "5879"
#> [41] "5880" "5881" "595" "60" "637"
#> [46] "6442" "6443" "6444" "6445" "71"
#> [51] "836" "841" "842" "857" "8672"
#> [56] "940" "941" "942" "958" "959"
#>
#> $`hsa04622_RIG-I-like_receptor_signaling_pathway`
#> [1] "10010" "1147" "1432" "1540" "1654" "23586" "26007"
#> [8] "29110" "338376" "340061" "3439" "3440" "3441" "3442"
#> [15] "3443" "3444" "3445" "3446" "3447" "3448" "3449"
#> [22] "3451" "3452" "3456" "3467" "3551" "3576" "3592"
#> [29] "3593" "3627" "3661" "3665" "4214" "4790" "4792"
#> [36] "4793" "5300" "54941" "55593" "5599" "5600" "5601"
#> [43] "5602" "5603" "56832" "57506" "5970" "6300" "64135"
#> [50] "64343" "6885" "7124" "7186" "7187" "7189" "7706"
#> [57] "79132" "79671" "80143" "841" "843" "8517" "8717"
#> [64] "8737" "8772" "9140" "9474" "9636" "9641" "9755"See also the MSigDb for additional gene set collections.
9.10 GO/KEGG overrepresentation analysis
A variety of gene set analysis methods have been proposed Khatri et al., 2012. The most basic, yet frequently used, method is the over-representation analysis (ORA) with gene sets defined according to GO or KEGG. As outlined in the first section, ORA tests the overlap between DE genes (typically DE p-value < 0.05) and genes in a gene set based on the hypergeometric distribution. Here, we choose a significance level \(\alpha = 0.2\) for demonstration.
ora.all <- sbea(method="ora", se=allSE, gs=hsa.gs, perm=0, alpha=0.2)
gsRanking(ora.all)
#> DataFrame with 7 rows and 4 columns
#> GENE.SET
#> <character>
#> 1 hsa05202_Transcriptional_misregulation_in_cancer
#> 2 hsa05412_Arrhythmogenic_right_ventricular_cardiomyopathy_(ARVC)
#> 3 hsa05144_Malaria
#> 4 hsa04670_Leukocyte_transendothelial_migration
#> 5 hsa05100_Bacterial_invasion_of_epithelial_cells
#> 6 hsa04622_RIG-I-like_receptor_signaling_pathway
#> 7 hsa05130_Pathogenic_Escherichia_coli_infection
#> NR.GENES NR.SIG.GENES P.VALUE
#> <numeric> <numeric> <numeric>
#> 1 153 17 0.0351
#> 2 63 8 0.0717
#> 3 45 6 0.0932
#> 4 94 10 0.122
#> 5 64 7 0.162
#> 6 54 6 0.178
#> 7 43 5 0.184Such a ranked list is the standard output of most existing enrichment tools. Using the eaBrowse function creates a HTML summary from which each gene set can be inspected in more detail.
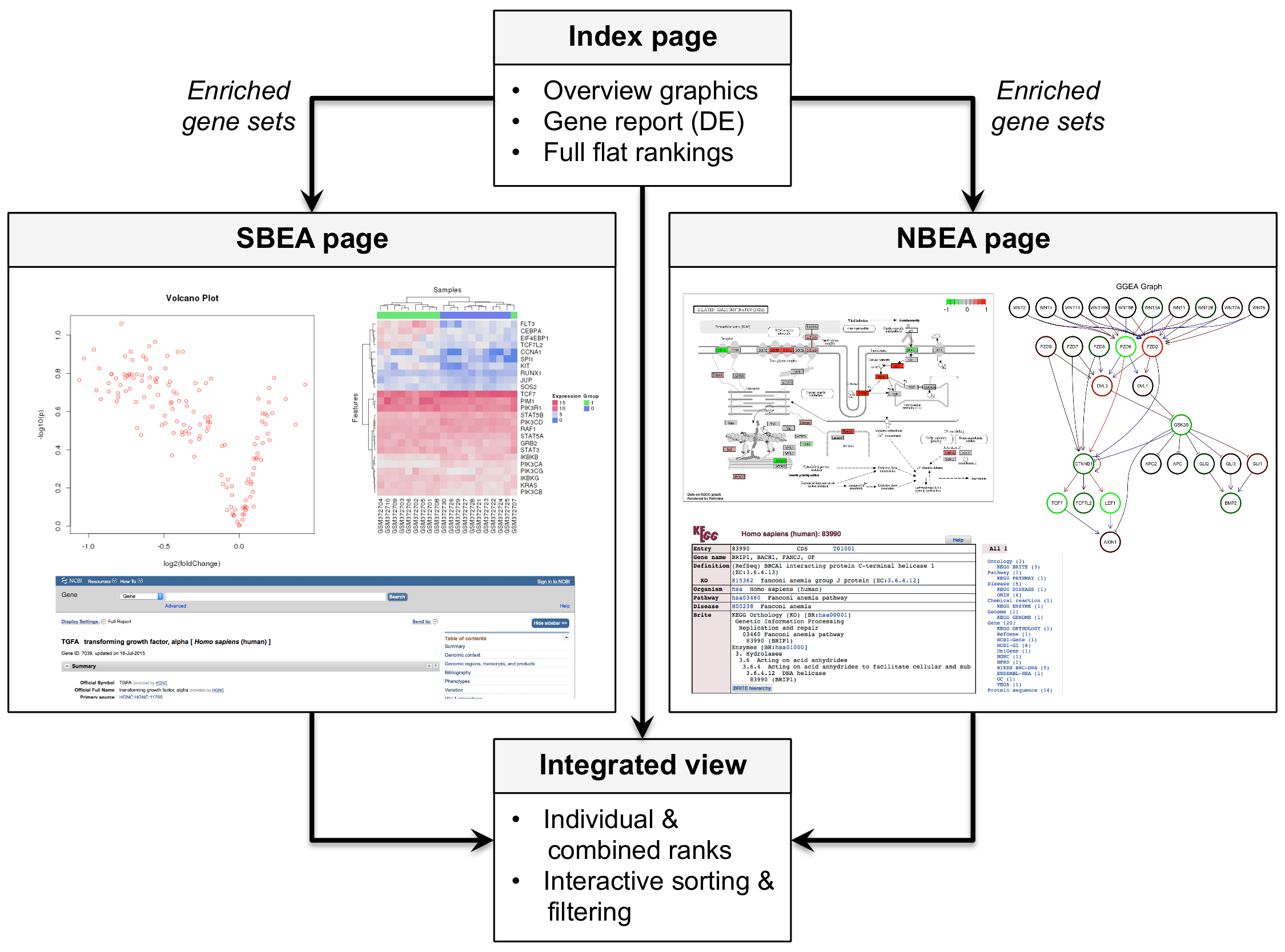
eaBrowse(ora.all)
#> Creating gene report ...
#>
#> Creating set view ...
#> Creating kegg view ...The resulting summary page includes for each significant gene set
- a gene report, which lists all genes of a set along with fold change and DE \(p\)-value (click on links in column
NR.GENES), - interactive overview plots such as heatmap and volcano plot (column
SET.VIEW, supports mouse-over and click-on), - for KEGG pathways: highlighting of differentially expressed genes on the pathway maps (column
PATH.VIEW, supports mouse-over and click-on).
As ORA works on the list of DE genes and not the actual expression values, it can be straightforward applied to RNA-seq data. However, as the gene sets here contain NCBI Entrez gene IDs and the airway dataset contains ENSEMBL gene ids, we first map the airway dataset to Entrez IDs.
airSE <- idMap(airSE, org="hsa", from="ENSEMBL", to="ENTREZID")
#> 'select()' returned 1:many mapping between keys and columns
#> Excluded 1133 genes without a corresponding to.ID
#> Encountered 8 from.IDs with >1 corresponding to.ID (a single to.ID was chosen for each of them)ora.air <- sbea(method="ora", se=airSE, gs=hsa.gs, perm=0)
gsRanking(ora.air)
#> DataFrame with 9 rows and 4 columns
#> GENE.SET
#> <character>
#> 1 hsa05206_MicroRNAs_in_cancer
#> 2 hsa05218_Melanoma
#> 3 hsa05214_Glioma
#> 4 hsa05131_Shigellosis
#> 5 hsa05410_Hypertrophic_cardiomyopathy_(HCM)
#> 6 hsa04670_Leukocyte_transendothelial_migration
#> 7 hsa05100_Bacterial_invasion_of_epithelial_cells
#> 8 hsa04514_Cell_adhesion_molecules_(CAMs)
#> 9 hsa05412_Arrhythmogenic_right_ventricular_cardiomyopathy_(ARVC)
#> NR.GENES NR.SIG.GENES P.VALUE
#> <numeric> <numeric> <numeric>
#> 1 118 68 0.000508
#> 2 50 33 0.000662
#> 3 48 30 0.00419
#> 4 53 31 0.0142
#> 5 53 31 0.0142
#> 6 62 34 0.0353
#> 7 60 33 0.036
#> 8 60 33 0.036
#> 9 48 27 0.0402Note #1: Young et al., 2010, have reported biased results for ORA on RNA-seq data due to over-detection of differential expression for long and highly expressed transcripts. The goseq package and limma::goana implement possibilities to adjust ORA for gene length and abundance bias.
Note #2: Independent of the expression data type under investigation, overlap between gene sets can result in redundant findings. This is well-documented for GO (parent-child structure, Rhee et al., 2008) and KEGG (pathway overlap/crosstalk, Donato et al., 2013). The topGO package (explicitly designed for GO) and mgsa (applicable to arbitrary gene set definitions) implement modifications of ORA to account for such redundancies.
9.11 Functional class scoring & permutation testing
A major limitation of ORA is that it restricts analysis to DE genes, excluding genes not satisfying the chosen significance threshold (typically the vast majority).
This is resolved by gene set enrichment analysis (GSEA), which scores the tendency of gene set members to appear rather at the top or bottom of the ranked list of all measured genes Subramanian et al., 2005. The statistical significance of the enrichment score (ES) of a gene set is assessed via sample permutation, i.e. (1) sample labels (= group assignment) are shuffled, (2) per-gene DE statistics are recomputed, and (3) the enrichment score is recomputed. Repeating this procedure many times allows to determine the empirical distribution of the enrichment score and to compare the observed enrichment score against it. Here, we carry out GSEA with 1000 permutations.
gsea.all <- sbea(method="gsea", se=allSE, gs=hsa.gs, perm=1000)
#> Permutations: 1 -- 100
#> Permutations: 101 -- 200
#> Permutations: 201 -- 300
#> Permutations: 301 -- 400
#> Permutations: 401 -- 500
#> Permutations: 501 -- 600
#> Permutations: 601 -- 700
#> Permutations: 701 -- 800
#> Permutations: 801 -- 900
#> Permutations: 901 -- 1000
#> Processing ...gsRanking(gsea.all)
#> DataFrame with 20 rows and 4 columns
#> GENE.SET
#> <character>
#> 1 hsa05412_Arrhythmogenic_right_ventricular_cardiomyopathy_(ARVC)
#> 2 hsa04670_Leukocyte_transendothelial_migration
#> 3 hsa04520_Adherens_junction
#> 4 hsa04390_Hippo_signaling_pathway
#> 5 hsa05323_Rheumatoid_arthritis
#> ... ...
#> 16 hsa05217_Basal_cell_carcinoma
#> 17 hsa04210_Apoptosis
#> 18 hsa05130_Pathogenic_Escherichia_coli_infection
#> 19 hsa05410_Hypertrophic_cardiomyopathy_(HCM)
#> 20 hsa05131_Shigellosis
#> ES NES P.VALUE
#> <numeric> <numeric> <numeric>
#> 1 0.511 1.92 0
#> 2 0.499 1.78 0
#> 3 0.488 1.74 0
#> 4 0.459 1.67 0
#> 5 0.574 1.66 0.0019
#> ... ... ... ...
#> 16 0.559 1.64 0.0248
#> 17 0.424 1.44 0.0336
#> 18 0.486 1.54 0.0347
#> 19 0.386 1.45 0.0406
#> 20 0.479 1.49 0.0436As GSEA’s permutation procedure involves re-computation of per-gene DE statistics, adaptations are necessary for RNA-seq. The EnrichmentBrowser implements an accordingly adapted version of GSEA, which allows incorporation of limma/voom, edgeR, or DESeq2 for repeated DE re-computation within GSEA. However, this is computationally intensive (for limma/voom the least, for DESeq2 the most). Note the relatively long running times for only 100 permutations having used edgeR for DE analysis.
gsea.air <- sbea(method="gsea", se=airSE, gs=hsa.gs, perm=100)
#> 100 permutations completedWhile it might be in some cases necessary to apply permutation-based GSEA for RNA-seq data, there are also alternatives avoiding permutation. Among them is ROtAtion gene Set Testing (ROAST), which uses rotation instead of permutation Wu et al., 2010.
roast.air <- sbea(method="roast", se=airSE, gs=hsa.gs)
gsRanking(roast.air)
#> DataFrame with 27 rows and 4 columns
#> GENE.SET NR.GENES DIR
#> <character> <numeric> <numeric>
#> 1 hsa05410_Hypertrophic_cardiomyopathy_(HCM) 53 1
#> 2 hsa05134_Legionellosis 35 1
#> 3 hsa05416_Viral_myocarditis 33 1
#> 4 hsa00790_Folate_biosynthesis 11 1
#> 5 hsa03030_DNA_replication 33 -1
#> ... ... ... ...
#> 23 hsa04150_mTOR_signaling_pathway 50 1
#> 24 hsa04350_TGF-beta_signaling_pathway 63 1
#> 25 hsa00561_Glycerolipid_metabolism 39 1
#> 26 hsa04621_NOD-like_receptor_signaling_pathway 40 -1
#> 27 hsa04514_Cell_adhesion_molecules_(CAMs) 60 -1
#> P.VALUE
#> <numeric>
#> 1 0.001
#> 2 0.001
#> 3 0.001
#> 4 0.001
#> 5 0.001
#> ... ...
#> 23 0.027
#> 24 0.029
#> 25 0.032
#> 26 0.033
#> 27 0.035A selection of additional methods is also available:
sbeaMethods()
#> [1] "ora" "safe" "gsea" "gsa" "padog"
#> [6] "globaltest" "roast" "camera" "gsva" "samgs"
#> [11] "ebm" "mgsa"Exercise: Carry out a GO overrepresentation analysis for the allSE and airSE. How many significant gene sets do you observe in each case?
9.12 Network-based enrichment analysis
Having found gene sets that show enrichment for differential expression, we are now interested whether these findings can be supported by known regulatory interactions.
For example, we want to know whether transcription factors and their target genes are expressed in accordance to the connecting regulations (activation/inhibition). Such information is usually given in a gene regulatory network derived from specific experiments or compiled from the literature (Geistlinger et al., 2013 for an example).
There are well-studied processes and organisms for which comprehensive and well-annotated regulatory networks are available, e.g. the RegulonDB for E. coli and Yeastract for S. cerevisiae.
However, there are also cases where such a network is missing or at least incomplete. A basic workaround is to compile a network from regulations in pathway databases such as KEGG.
hsa.grn <- compileGRN(org="hsa", db="kegg")
head(hsa.grn)
#> FROM TO TYPE
#> [1,] "10000" "100132074" "-"
#> [2,] "10000" "1026" "-"
#> [3,] "10000" "1026" "+"
#> [4,] "10000" "1027" "-"
#> [5,] "10000" "10488" "+"
#> [6,] "10000" "107" "+"Signaling pathway impact analysis (SPIA) is a network-based enrichment analysis method, which is explicitly designed for KEGG signaling pathways Tarca et al., 2009. The method evaluates whether expression changes are propagated across the pathway topology in combination with ORA.
spia.all <- nbea(method="spia", se=allSE, gs=hsa.gs, grn=hsa.grn, alpha=0.2)
#>
#> Done pathway 1 : RNA transport..
#> Done pathway 2 : RNA degradation..
#> Done pathway 3 : PPAR signaling pathway..
#> Done pathway 4 : Fanconi anemia pathway..
#> Done pathway 5 : MAPK signaling pathway..
#> Done pathway 6 : ErbB signaling pathway..
#> Done pathway 7 : Calcium signaling pathway..
#> Done pathway 8 : Cytokine-cytokine receptor int..
#> Done pathway 9 : Chemokine signaling pathway..
#> Done pathway 10 : NF-kappa B signaling pathway..
#> Done pathway 11 : Phosphatidylinositol signaling..
#> Done pathway 12 : Neuroactive ligand-receptor in..
#> Done pathway 13 : Cell cycle..
#> Done pathway 14 : Oocyte meiosis..
#> Done pathway 15 : p53 signaling pathway..
#> Done pathway 16 : Sulfur relay system..
#> Done pathway 17 : SNARE interactions in vesicula..
#> Done pathway 18 : Regulation of autophagy..
#> Done pathway 19 : Protein processing in endoplas..
#> Done pathway 20 : Lysosome..
#> Done pathway 21 : mTOR signaling pathway..
#> Done pathway 22 : Apoptosis..
#> Done pathway 23 : Vascular smooth muscle contrac..
#> Done pathway 24 : Wnt signaling pathway..
#> Done pathway 25 : Dorso-ventral axis formation..
#> Done pathway 26 : Notch signaling pathway..
#> Done pathway 27 : Hedgehog signaling pathway..
#> Done pathway 28 : TGF-beta signaling pathway..
#> Done pathway 29 : Axon guidance..
#> Done pathway 30 : VEGF signaling pathway..
#> Done pathway 31 : Osteoclast differentiation..
#> Done pathway 32 : Focal adhesion..
#> Done pathway 33 : ECM-receptor interaction..
#> Done pathway 34 : Cell adhesion molecules (CAMs)..
#> Done pathway 35 : Adherens junction..
#> Done pathway 36 : Tight junction..
#> Done pathway 37 : Gap junction..
#> Done pathway 38 : Complement and coagulation cas..
#> Done pathway 39 : Antigen processing and present..
#> Done pathway 40 : Toll-like receptor signaling p..
#> Done pathway 41 : NOD-like receptor signaling pa..
#> Done pathway 42 : RIG-I-like receptor signaling ..
#> Done pathway 43 : Cytosolic DNA-sensing pathway..
#> Done pathway 44 : Jak-STAT signaling pathway..
#> Done pathway 45 : Natural killer cell mediated c..
#> Done pathway 46 : T cell receptor signaling path..
#> Done pathway 47 : B cell receptor signaling path..
#> Done pathway 48 : Fc epsilon RI signaling pathwa..
#> Done pathway 49 : Fc gamma R-mediated phagocytos..
#> Done pathway 50 : Leukocyte transendothelial mig..
#> Done pathway 51 : Intestinal immune network for ..
#> Done pathway 52 : Circadian rhythm - mammal..
#> Done pathway 53 : Long-term potentiation..
#> Done pathway 54 : Neurotrophin signaling pathway..
#> Done pathway 55 : Retrograde endocannabinoid sig..
#> Done pathway 56 : Glutamatergic synapse..
#> Done pathway 57 : Cholinergic synapse..
#> Done pathway 58 : Serotonergic synapse..
#> Done pathway 59 : GABAergic synapse..
#> Done pathway 60 : Dopaminergic synapse..
#> Done pathway 61 : Long-term depression..
#> Done pathway 62 : Olfactory transduction..
#> Done pathway 63 : Taste transduction..
#> Done pathway 64 : Phototransduction..
#> Done pathway 65 : Regulation of actin cytoskelet..
#> Done pathway 66 : Insulin signaling pathway..
#> Done pathway 67 : GnRH signaling pathway..
#> Done pathway 68 : Progesterone-mediated oocyte m..
#> Done pathway 69 : Melanogenesis..
#> Done pathway 70 : Adipocytokine signaling pathwa..
#> Done pathway 71 : Type II diabetes mellitus..
#> Done pathway 72 : Type I diabetes mellitus..
#> Done pathway 73 : Maturity onset diabetes of the..
#> Done pathway 74 : Aldosterone-regulated sodium r..
#> Done pathway 75 : Endocrine and other factor-reg..
#> Done pathway 76 : Vasopressin-regulated water re..
#> Done pathway 77 : Salivary secretion..
#> Done pathway 78 : Gastric acid secretion..
#> Done pathway 79 : Pancreatic secretion..
#> Done pathway 80 : Carbohydrate digestion and abs..
#> Done pathway 81 : Bile secretion..
#> Done pathway 82 : Mineral absorption..
#> Done pathway 83 : Alzheimer's disease..
#> Done pathway 84 : Parkinson's disease..
#> Done pathway 85 : Amyotrophic lateral sclerosis ..
#> Done pathway 86 : Huntington's disease..
#> Done pathway 87 : Prion diseases..
#> Done pathway 88 : Cocaine addiction..
#> Done pathway 89 : Amphetamine addiction..
#> Done pathway 90 : Morphine addiction..
#> Done pathway 91 : Alcoholism..
#> Done pathway 92 : Bacterial invasion of epitheli..
#> Done pathway 93 : Vibrio cholerae infection..
#> Done pathway 94 : Epithelial cell signaling in H..
#> Done pathway 95 : Pathogenic Escherichia coli in..
#> Done pathway 96 : Shigellosis..
#> Done pathway 97 : Salmonella infection..
#> Done pathway 98 : Pertussis..
#> Done pathway 99 : Legionellosis..
#> Done pathway 100 : Leishmaniasis..
#> Done pathway 101 : Chagas disease (American trypa..
#> Done pathway 102 : African trypanosomiasis..
#> Done pathway 103 : Malaria..
#> Done pathway 104 : Toxoplasmosis..
#> Done pathway 105 : Amoebiasis..
#> Done pathway 106 : Staphylococcus aureus infectio..
#> Done pathway 107 : Tuberculosis..
#> Done pathway 108 : Hepatitis C..
#> Done pathway 109 : Measles..
#> Done pathway 110 : Influenza A..
#> Done pathway 111 : HTLV-I infection..
#> Done pathway 112 : Herpes simplex infection..
#> Done pathway 113 : Epstein-Barr virus infection..
#> Done pathway 114 : Pathways in cancer..
#> Done pathway 115 : Transcriptional misregulation ..
#> Done pathway 116 : Viral carcinogenesis..
#> Done pathway 117 : Colorectal cancer..
#> Done pathway 118 : Renal cell carcinoma..
#> Done pathway 119 : Pancreatic cancer..
#> Done pathway 120 : Endometrial cancer..
#> Done pathway 121 : Glioma..
#> Done pathway 122 : Prostate cancer..
#> Done pathway 123 : Thyroid cancer..
#> Done pathway 124 : Basal cell carcinoma..
#> Done pathway 125 : Melanoma..
#> Done pathway 126 : Bladder cancer..
#> Done pathway 127 : Chronic myeloid leukemia..
#> Done pathway 128 : Acute myeloid leukemia..
#> Done pathway 129 : Small cell lung cancer..
#> Done pathway 130 : Non-small cell lung cancer..
#> Done pathway 131 : Asthma..
#> Done pathway 132 : Autoimmune thyroid disease..
#> Done pathway 133 : Systemic lupus erythematosus..
#> Done pathway 134 : Rheumatoid arthritis..
#> Done pathway 135 : Allograft rejection..
#> Done pathway 136 : Graft-versus-host disease..
#> Done pathway 137 : Arrhythmogenic right ventricul..
#> Done pathway 138 : Dilated cardiomyopathy..
#> Done pathway 139 : Viral myocarditis..
#> Finished SPIA analysis
gsRanking(spia.all)
#> DataFrame with 7 rows and 6 columns
#> GENE.SET SIZE NDE
#> <character> <numeric> <numeric>
#> 1 hsa04620_Toll-like_receptor_signaling_pathway 74 6
#> 2 hsa05202_Transcriptional_misregulation_in_cancer 89 9
#> 3 hsa05416_Viral_myocarditis 45 5
#> 4 hsa04630_Jak-STAT_signaling_pathway 72 8
#> 5 hsa04910_Insulin_signaling_pathway 115 5
#> 6 hsa05143_African_trypanosomiasis 22 4
#> 7 hsa04978_Mineral_absorption 3 1
#> T.ACT STATUS P.VALUE
#> <numeric> <numeric> <numeric>
#> 1 -3.62 -1 0.0497
#> 2 -0.209 -1 0.0726
#> 3 2.98 1 0.0768
#> 4 -1.06 -1 0.0861
#> 5 -7.35 -1 0.153
#> 6 0.263 1 0.193
#> 7 0 -1 0.199More generally applicable is gene graph enrichment analysis (GGEA), which evaluates consistency of interactions in a given gene regulatory network with the observed expression data Geistlinger et al., 2011.
ggea.all <- nbea(method="ggea", se=allSE, gs=hsa.gs, grn=hsa.grn)
gsRanking(ggea.all)
#> DataFrame with 9 rows and 5 columns
#> GENE.SET
#> <character>
#> 1 hsa04390_Hippo_signaling_pathway
#> 2 hsa05416_Viral_myocarditis
#> 3 hsa05217_Basal_cell_carcinoma
#> 4 hsa04520_Adherens_junction
#> 5 hsa04350_TGF-beta_signaling_pathway
#> 6 hsa05412_Arrhythmogenic_right_ventricular_cardiomyopathy_(ARVC)
#> 7 hsa04910_Insulin_signaling_pathway
#> 8 hsa04622_RIG-I-like_receptor_signaling_pathway
#> 9 hsa04210_Apoptosis
#> NR.RELS RAW.SCORE NORM.SCORE P.VALUE
#> <numeric> <numeric> <numeric> <numeric>
#> 1 62 22.8 0.367 0.002
#> 2 7 3.3 0.471 0.003
#> 3 18 6.92 0.385 0.00799
#> 4 11 4.5 0.409 0.014
#> 5 14 5.36 0.383 0.024
#> 6 4 1.75 0.437 0.032
#> 7 31 11.1 0.359 0.039
#> 8 35 12.5 0.356 0.041
#> 9 47 16.5 0.35 0.044nbeaMethods()
#> [1] "ggea" "spia" "pathnet" "degraph" "ganpa"
#> [6] "cepa" "topologygsa" "netgsa"Note #1: As network-based enrichment methods typically do not involve sample permutation but rather network permutation, thus avoiding DE re-computation, they can likewise be applied to RNA-seq data.
Note #2: Given the various enrichment methods with individual benefits and limitations, combining multiple methods can be beneficial, e.g. combined application of a set-based and a network-based method. This has been shown to filter out spurious hits of individual methods and to reduce the outcome to gene sets accumulating evidence from different methods Geistlinger et al., 2016, Alhamdoosh et al., 2017.
The function combResults implements the straightforward combination of results, thereby facilitating seamless comparison of results across methods. For demonstration, we use the ORA and GSEA results for the ALL dataset from the previous section:
res.list <- list(ora.all, gsea.all)
comb.res <- combResults(res.list)
gsRanking(comb.res)
#> DataFrame with 20 rows and 6 columns
#> GENE.SET
#> <character>
#> 1 hsa05412_Arrhythmogenic_right_ventricular_cardiomyopathy_(ARVC)
#> 2 hsa05202_Transcriptional_misregulation_in_cancer
#> 3 hsa04670_Leukocyte_transendothelial_migration
#> 4 hsa04520_Adherens_junction
#> 5 hsa05206_MicroRNAs_in_cancer
#> ... ...
#> 16 hsa05410_Hypertrophic_cardiomyopathy_(HCM)
#> 17 hsa04514_Cell_adhesion_molecules_(CAMs)
#> 18 hsa04621_NOD-like_receptor_signaling_pathway
#> 19 hsa04622_RIG-I-like_receptor_signaling_pathway
#> 20 hsa04350_TGF-beta_signaling_pathway
#> ORA.RANK GSEA.RANK MEAN.RANK ORA.PVAL GSEA.PVAL
#> <numeric> <numeric> <numeric> <numeric> <numeric>
#> 1 5.1 10.3 7.7 0.0717 0
#> 2 2.6 17.9 10.3 0.0351 0.00374
#> 3 10.3 10.3 10.3 0.122 0
#> 4 20.5 10.3 15.4 0.201 0
#> 5 23.1 25.6 24.4 0.225 0.00781
#> ... ... ... ... ... ...
#> 16 41 48.7 44.9 0.403 0.0406
#> 17 69.2 23.1 46.2 0.649 0.0058
#> 18 61.5 33.3 47.4 0.631 0.0172
#> 19 15.4 84.6 50 0.178 0.354
#> 20 38.5 61.5 50 0.39 0.113Exercise: Carry out SPIA and GGEA for the airSE and combine the results. How many gene sets are rendered significant by both methods?
9.13 Genomic region enrichment analysis
Microarrays and next-generation sequencing are also widely applied for large-scale detection of variable and regulatory genomic regions, e.g. single nucleotide polymorphisms, copy number variations, and transcription factor binding sites.
Such experimentally-derived genomic region sets are raising similar questions regarding functional enrichment as in gene expression data analysis.
Of particular interest is thereby whether experimentally-derived regions overlap more (enrichment) or less (depletion) than expected by chance with regions representing known functional features such as genes or promoters.
The regioneR package implements a general framework for testing overlaps of genomic regions based on permutation sampling. This allows to repeatedly sample random regions from the genome, matching size and chromosomal distribution of the region set under study. By recomputing the overlap with the functional features in each permutation, statistical significance of the observed overlap can be assessed.
suppressPackageStartupMessages(library(regioneR))To demonstrate the basic functionality of the package, we consider the overlap of gene promoter regions and CpG islands in the human genome. We expect to find an enrichment as promoter regions are known to be GC-rich. Hence, is the overlap between CpG islands and promoters greater than expected by chance?
We use the collection of CpG islands described in Wu et al., 2010 and restrict them to the set of canonical chromosomes 1-23, X, and Y.
cpgHMM <- toGRanges("http://www.haowulab.org/software/makeCGI/model-based-cpg-islands-hg19.txt")
cpgHMM <- filterChromosomes(cpgHMM, chr.type="canonical")
cpgHMM <- sort(cpgHMM)
cpgHMM
#> GRanges object with 63705 ranges and 5 metadata columns:
#> seqnames ranges strand | length CpGcount
#> <Rle> <IRanges> <Rle> | <integer> <integer>
#> [1] chr1 10497-11241 * | 745 110
#> [2] chr1 28705-29791 * | 1087 115
#> [3] chr1 135086-135805 * | 720 42
#> [4] chr1 136164-137362 * | 1199 71
#> [5] chr1 137665-138121 * | 457 22
#> ... ... ... ... . ... ...
#> [63701] chrY 59213702-59214290 * | 589 43
#> [63702] chrY 59240512-59241057 * | 546 40
#> [63703] chrY 59348047-59348370 * | 324 17
#> [63704] chrY 59349137-59349565 * | 429 31
#> [63705] chrY 59361489-59362401 * | 913 128
#> GCcontent pctGC obsExp
#> <integer> <numeric> <numeric>
#> [1] 549 0.737 1.106
#> [2] 792 0.729 0.818
#> [3] 484 0.672 0.548
#> [4] 832 0.694 0.524
#> [5] 301 0.659 0.475
#> ... ... ... ...
#> [63701] 366 0.621 0.765
#> [63702] 369 0.676 0.643
#> [63703] 193 0.596 0.593
#> [63704] 276 0.643 0.7
#> [63705] 650 0.712 1.108
#> -------
#> seqinfo: 24 sequences from an unspecified genome; no seqlengthsAnalogously, we load promoter regions in the hg19 human genome assembly as available from UCSC:
promoters <- toGRanges("http://gattaca.imppc.org/regioner/data/UCSC.promoters.hg19.bed")
promoters <- filterChromosomes(promoters, chr.type="canonical")
promoters <- sort(promoters)
promoters
#> GRanges object with 49049 ranges and 3 metadata columns:
#> seqnames ranges strand | V4 V5 V6
#> <Rle> <IRanges> <Rle> | <factor> <factor> <factor>
#> [1] chr1 9873-12073 * | TSS . +
#> [2] chr1 16565-18765 * | TSS . -
#> [3] chr1 17551-19751 * | TSS . -
#> [4] chr1 17861-20061 * | TSS . -
#> [5] chr1 19559-21759 * | TSS . -
#> ... ... ... ... . ... ... ...
#> [49045] chrY 59211948-59214148 * | TSS . +
#> [49046] chrY 59328251-59330451 * | TSS . +
#> [49047] chrY 59350972-59353172 * | TSS . +
#> [49048] chrY 59352984-59355184 * | TSS . +
#> [49049] chrY 59360654-59362854 * | TSS . -
#> -------
#> seqinfo: 24 sequences from an unspecified genome; no seqlengthsTo speed up the example, we restrict analysis to chromosomes 21 and 22. Note that this is done for demonstration only. To make an accurate claim, the complete region set should be used (which, however, runs considerably longer).
cpg <- cpgHMM[seqnames(cpgHMM) %in% c("chr21", "chr22")]
prom <- promoters[seqnames(promoters) %in% c("chr21", "chr22")]Now, we are applying an overlap permutation test with 100 permutations (ntimes=100), while maintaining chromosomal distribution of the CpG island region set (per.chromosome=TRUE). Furthermore, we use the option count.once=TRUE to count an overlapping CpG island only once, even if it overlaps with 2 or more promoters.
Note that we use 100 permutations for demonstration only. To draw robust conclusions a minimum of 1000 permutations should be carried out.
pt <- overlapPermTest(cpg, prom, genome="hg19", ntimes=100, per.chromosome=TRUE, count.once=TRUE)
pt
#> $numOverlaps
#> P-value: 0.0099009900990099
#> Z-score: 43.4132
#> Number of iterations: 100
#> Alternative: greater
#> Evaluation of the original region set: 719
#> Evaluation function: numOverlaps
#> Randomization function: randomizeRegions
#>
#> attr(,"class")
#> [1] "permTestResultsList"summary(pt[[1]]$permuted)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 145.0 162.0 171.0 171.6 179.2 209.0The resulting permutation p-value indicates a significant enrichment. Out of the 2859 CpG islands, 719 overlap with at least one promoter. In contrast, when repeatedly drawing random regions matching the CpG islands in size and chromosomal distribution, the mean number of overlapping regions across permutations was 117.7 \(\pm\) 11.8.
Note #1: The function regioneR::permTest allows to incorporate user-defined functions for randomizing regions and evaluating additional measures of overlap such as total genomic size in bp.
Note #2: The LOLA package implements a genomic region ORA, which assesses genomic region overlap based on the hypergeometric distribution using a library of pre-defined functional region sets.